快手因果推断与实验设计

[ 导读 ]理解和识别用户行为指标的相互关系是实验分析的目标。在社区氛围下，影响用户行为的因素更为复杂，关系识别更为困难，如何使用各种学科的方法，对社区进行宏观或微观的建模分析，系统性的评估各种策略的长期生态影响，是所要解决的重要问题。

本文金雅然博士将以快手直播的现实任务为例进行展开，介绍快手因果推断与实验设计的相关工作，主要内容包括：① 快手直播场景中遇到的因果推断问题及技术框架；② 基于观测数据或实验数据的因果推断技术案例；③ 涉及到网络效应的复杂实验设计。

01 快手直播场景中遇到的因果推断问题及技术框架

在快手我们主要会遇到这四类问题：用户激励设计、推荐策略评估、产品功能迭代以及预估产品和方向的长期价值。

遇到这些问题我们通常有几种方式来解决：

• 基于观测数据的因果推断，即从已有实验和非实验数据中提炼因果关系；
• 在产品设计上构建正确的AB实验，合理计算指标，度量产品功能和迭代的影响；
• 通过经济模型、机器学习算法和数据、实验的结合构造反事实推理来回答长期效应问题。

解决这些问题的核心是使用因果推断方法。

因果推断的核心是在数据中存在关联关系的前提下，考虑数据之间的因果关系。任务是在给定的假设中，选择模型框架，将因果关系从关联中分割，对因果分析的大小作出正确的估计，并且通过统计推断的方法，验证推断的正确度，并回答推断结果存在多大波动。

在因果推断中，我们通常应用以下两种框架：

Rubin虚拟事实模型（Potential Outcome）的核心是寻找合适的对照组。通常情况下，我们想要度量用户是否被实验影响到的两者差异是多少，而对于同一个用户，我们只能观测到被影响/不被影响一个状态，因此需要寻找合适的对照组，估计无法被观测到的影响。我们通常会构造一些识别实验，比如，经济学上通过RCT实验，互联网常使用AB实验，或者根据观测数据使用恰当的方法来寻找对照组。

Pearl因果图模型（Causal Graph Model）使用有向图描述变量之间的因果关系。通过计算因果图中的条件分布，获得变量之间的因果关系。有向图指导我们使用这些条件分布来消除估计偏差，其核心也是估计检验分布、消除其他变量带来的偏差。

Pearl框架和Rubin框架有一些关联，简单图中，Potential Outcome模型中通过工具变量和匹配法消除估计偏差和Pearl的框架思想是一致的。

但是Pearl的框架可以处理多个变量之间相互作用的复杂关系。

总结来说，Potential Outcome和Causal Graph是两种互补的推测虚拟事实的方法，目的都是为了计算存在混淆变量时，干预变量时对结果的影响，都需要对因果关系作假设，以及控制带来偏差的变量；不同点在于Rubin框架估计的因果效应主要是干预前后的期望差值，而Pearl框架下，我们估计的是干预前后的分布差异，Rubin框架解决的问题是因果效应的估计和统计推断，Pearl框架更偏向于因果关系的识别。

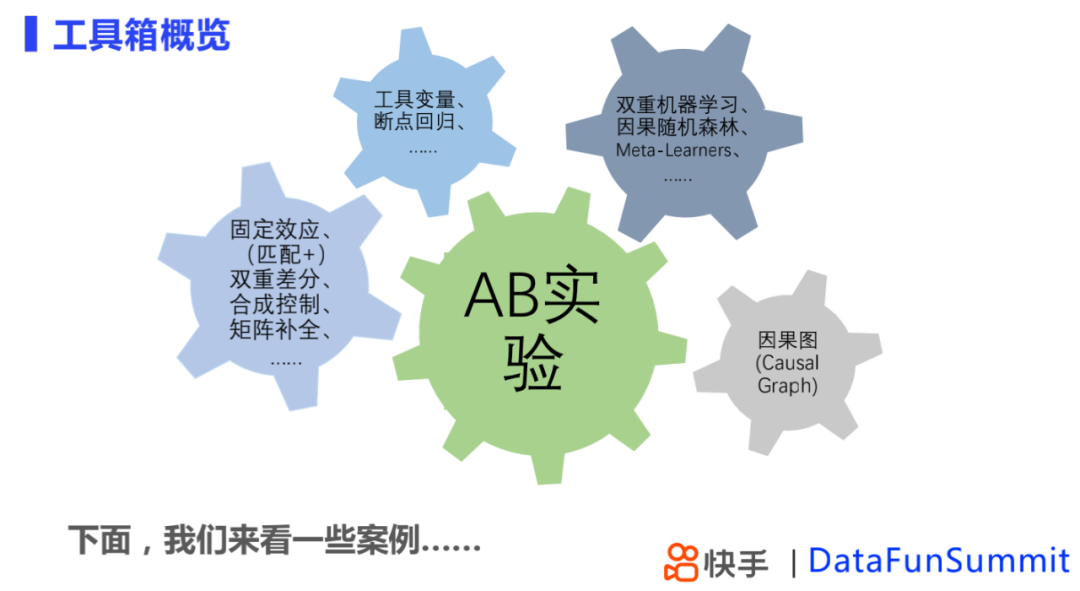
从这两种框架延伸，在不同情景下，快手会使用不同工具解决实际问题，AB实验帮助我们观测策略或产品变动影响，在一些不能做实验或者多个实验相结合的场景下，会有一些其他的方法，下面会对具体方法展开介绍。

02 基于观测数据或实验数据的因果推断技术案例

1. 产品功能的评估：DID及其拓展案例

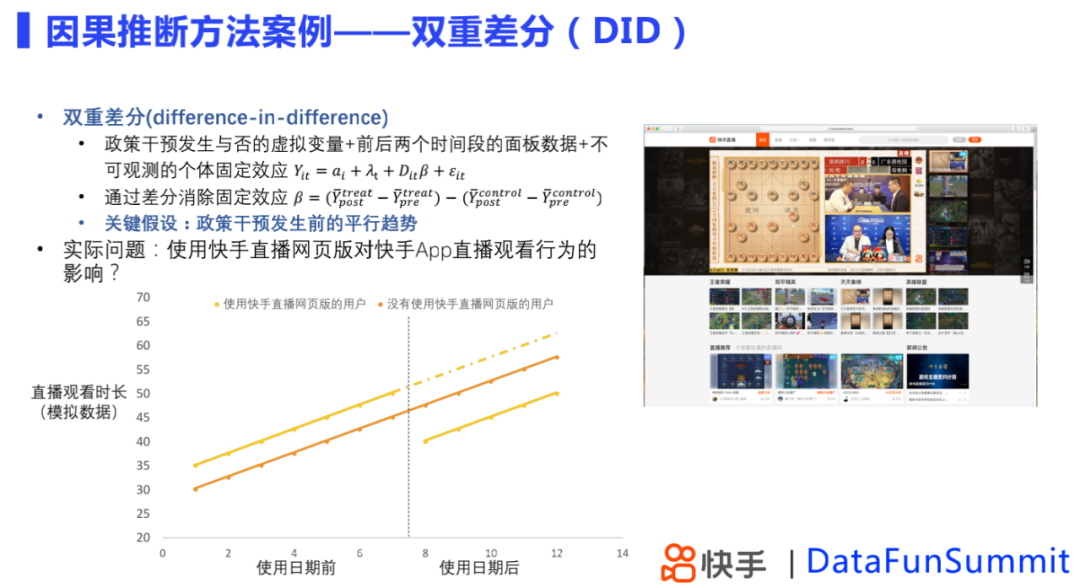
双重差分适用于存在不可观测的个体固定效应场景，通过差分消除固定效应，其关键假设是，政策干扰前存在平行趋势，且实验干扰效应不随时间变化。双重差分可以用来消除那些对后期可能存在干扰因素，得到实验效果估计。

双重差分假设用户开始受影响的时间是一样的，实验处理效应对用户的影响是一样的，而这些假设难以满足。比如穿云箭红包，当实验效果上线后，用户的行为会发生变化，且不同用户的行为是不一致的，当不同表现用户都在实验组，传统的DID模型估计实验效应会产生偏差。因此我们在DID方法上进行修正，按照用户的状态是否更改分为不同类型，对不同类型用户分别做DID估计，再进行加权平均，得到修正后DID实验效果值。

当treatment施加到一个群体或者地区上时，很难找到单一的对照组，这种时候采用合成控制方法构造虚拟对照组进行比较，原理是构造一个虚拟的对照组，通过treatment前的数据上学习的权重，拟合实验组在实验开始前的数据，模拟实验组用户在没有接受实验情况下的结果，构造合成控制组，实验开始后，评估实验组和合成控制组之间的差异。

2. 推荐策略的评估：因果推断与机器学习

因果分析与机器学习存在一些差异点。因果分析的语言，核心在于因果关系的识别，即合理的估计处理前和处理后现有条件期望的差异，也可以是一种处理缺失数据的问题，在因果推断上我们非常关心的是如何准确的估计结果以及结果的方差。而在机器学习中，我们使用准确度来衡量机器学习模型的好坏，其目标是在训练集上估计一个条件期望，使得测试集上MSE*小。机器学习可以通过cross-validation（模型参数）的方法去数据驱动的选择一个*佳模型形式，与传统计量经济学方法相比不需要复杂的假设，例如function form的假设，从这种意义上机器学习能够更准确的预测。

但是在因果推断问题上，机器学习的局限性在于，无论用什么机器学习方法，因果识别的条件都不能被放松；同时在机器学习模型通常使用的正则化和过拟合处理，会带来有偏估计，因此我们需要消除这种估计的偏差；在统计推断上，机器学习的局限性在于，有些模型不能直接计算方差，并且有时即使可以计算，方差的收敛速度也未必能够达到预期，所以针对这些问题，下面介绍了几种方法。

• ① 双重机器学习模型

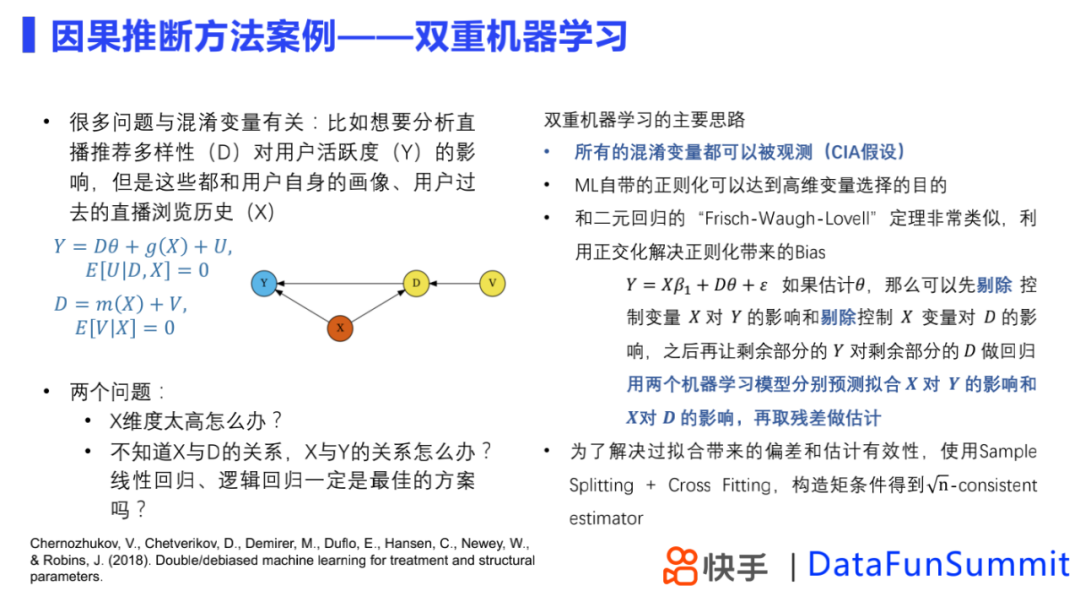
很多时候因果推断会遇到混淆变量的问题，比如想要去分析直播推荐多样性对用户活跃度的影响，但是这些都和用户历史相关。传统计量经济学方法可以解决这个问题，但是依赖很多强假设，强假设下，得到的估计不一定合理，双重机器学习为这个问题提供了解决的思路。

双重机器学习假设所有混淆变量都可以被观测，其正则化过程能够达到高维变量选择的目的，与Frisch-Waugh-Lovell定理相似，模型通过正交化解决正则化带来的偏差。

除了上面所描述的，还有一些问题待解决，比如在ML模型下存在偏差和估计有效性的问题，这个时候可以通过Sample Splitting 和 Cross Fitting的方式来解决，具体做法是我们把数据分成一个训练集和估计集，在训练集上我们分别使用机器学习来拟合影响，在估计集上我们根据拟合得到的函数来做残差的估计，通过这种方法，可以对偏差进行修正。在偏差修正的基础上，我们可以对整个估计方法去构造一个moment condition，得到置信区间的推断，从而得到一个有良好统计的估计。

• ② 因果随机森林模型

我们通常探究策略对于不同用户异质性的影响，即哪些用户更容易被影响以及影响有多大，传统做法是多维分析，但是效率低，容易犯错。这时可以结合机器学习的方法，这里选择了决策树方法，因为决策树的分桶特性能够帮助解决异质性问题，相对于传统方法因果树做了两点改动：

• 把数据分成训练集和估计集，一部分训练集去构造树，另一部分估计集去估计因果效应和方差；
• 在树的分区方式上，使用各个节点的方差对目标函数加以修正。

通常情况下，我们结合实验来做分析。比如在实验中，通过因果树得到因果效应的分布，然后挑选出来那些实验效果显著的用户，去分析他们的特征，以及找到敏感用户，帮助我们了解策略的影响，作出下一步迭代。

• ③ Meta-Learner for Uplift Modeling

Uplift-modeling是另一种定位敏感人群的方法，和因果树的步骤有差别。核心是利用实验数据对实验结果变量建模，利用得到的模型估计条件平均处理效果。Uplift-modeling具有不同的学习方式，主要有S-Learner 、T-Learner和X-learner。和因果树相比，Meta-Learner是一种间接建模方式，实现快但一些场景下误差较大。

3. 用户行为链路的研究：因果图

我们通常通过因果图来进行用户行为链路的研究。Rubin流派常用来估计变量之间的一度关系，但当我们面对一些未知问题时，我们想了解的是有哪些变量真正影响我们关心的结果变量，以及变量之间的相互影响和用户行为链路是什么，有效过程指标是什么，这些时候我们用到因果图的方法。

在生成因果图中，常遇到的限制是算法层面的，比如我们在优化目标函数的时候，需要遍历所有的因果图，是一个NP-hard问题，我们需要有效的算法得到想要的估计，市面上的算法大概分为两类：

• Constraint-based Algorithms
• Score-based Algorithms

03 复杂实验设计

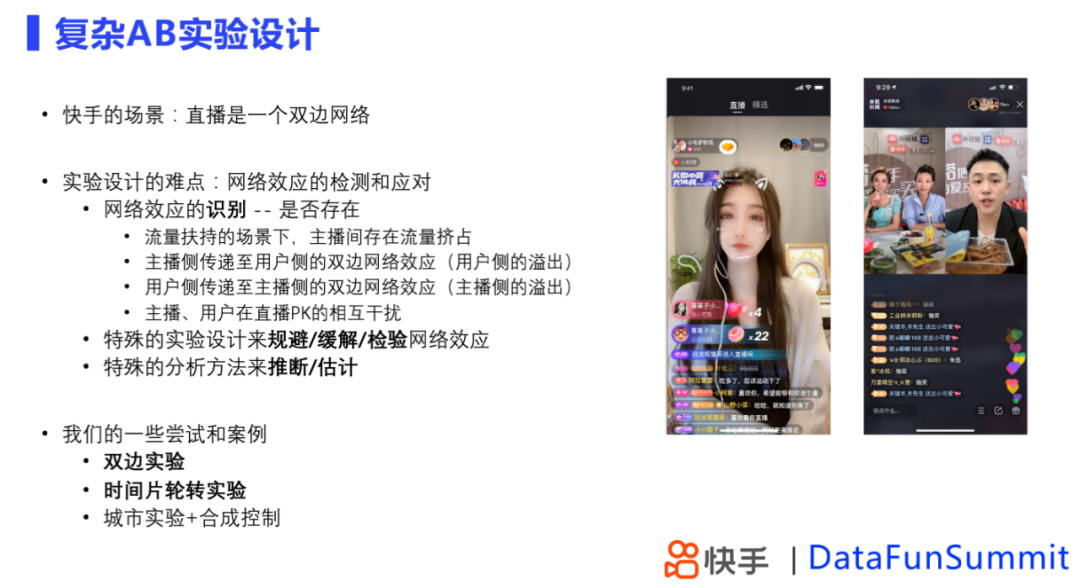
在实验设计上我们通常遇到的难点是网络效应的检测和应对，在直播下，网络效应有好多种表现方式，在这种网络效应存在的情况下尝试了一些方式，比如说：双边实验、时间片轮转实验、合成控制方法。

1. 双边实验设计

在双边实验中，同时进行了主播侧和观众侧的分流，主播侧一部分是上了挂件，观众侧一部分能看到一部分看不到，双边实验的优点是可以同时检测两端的效果，同时可以帮助检测到组间的转移和溢出。在了解到组间溢出和干扰下，通过双边实验我们可以更加准确的测算处理效应，在挂件场景下，我们认为N3是代表完全没有处理过的效果，Y代表处理后的结果，N3和Y进行差分，计算产品功能推全后的影响，而且，双边实验能够更好的帮助我们归因。

然而双边实验只能描述简单的组间溢出，在个体和个体之间存在干扰的复杂情况下，双边实验是无法帮助我们判断实验效果，例如直播PK暴击时刻这种情况下，我们通过时间片轮转实验解决，即在一定实验对象上进行实验组策略和对照组策略的反复切换。

2. 时间片轮转实验

时间片轮转的核心在于：

• 时间片的选择
• 实验总周期选择
• 随机切换时间点是什么样子的

当时间粒度约粗糙，时间上的干扰造成的偏差会越小，但是方差会越大，影响实验的检验效果，针对这个问题，采取的方案是*优设计。

*优设计的核心假设是：

• Outcome有一个*对上界
• 用户无法知晓下一个时间是否是实验组
• 如果时间片之间存在干扰，干扰的影响是固定且有限的